ガウス積分は数理統計学や統計物理学等に良く出てくる積分量で
| (1) |
となるものである。以下ではこれを導いてみる。
導出
まず ![]() として、この二乗を考える。ここで一つ目と二つ目の積分で積分変数を変えてある。定積分において積分変数は自由に変えても問題無かったからだ。
として、この二乗を考える。ここで一つ目と二つ目の積分で積分変数を変えてある。定積分において積分変数は自由に変えても問題無かったからだ。
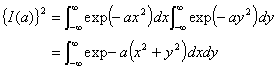 |
(2) |
となる。これを(平面における)極座標系に書き換える。(問)極座標系へ積分変数と積分範囲を書き換えよ。この様にせずに普通に2乗を計算してもうまく積分できない。
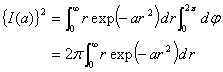 |
(3) |
となる。さらに r 2 = u と置けば(置換積分する)、
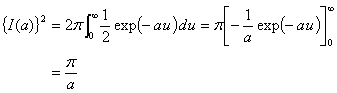 |
(4) |
となり求まった。
もう一歩進んで
ここでは統計物理学などで良く出る積分
| (5) |
について考えます。ただし n =1,2,3… とする。部分積分を繰り返しても求めることは出来ますが、(1)式の両辺をパラメター a について微分する事で求めたいと思います。(1)式の両辺を1回微分すると
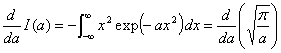 |
(6) |
となるのでこれを整理して
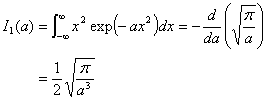 |
(7) |
が得られます。統計物理学などでこの(7)式を必要とする計算が現れます。さらに n 回微分を考えると
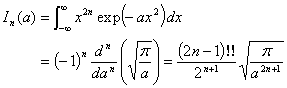 |
(8) |
を導く事が出来ます。(問)最後の等式を数学的帰納法で証明せよ。
ちなみに
♠ 次の積分が成り立つ事を示せ。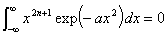 ヒント:被積分関数は偶関数か奇関数か。
ヒント:被積分関数は偶関数か奇関数か。
♠ 次の積分を計算せよ。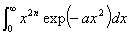 ヒント:被積分関数は偶関数か奇関数か。
ヒント:被積分関数は偶関数か奇関数か。
答え:答えは被積分関数が偶関数だから(8)式の半分になる。
答え:答えは被積分関数が偶関数だから(8)式の半分になる。
関連項目
置換積分|重積分|座標変換|ボルツマン因子