物の位置を表すのに「ここ」とか「あそこ」とか言っていたのでは話にならない。一意的に場所を指定したい。空間の中の場所を指定するのに物理で良く使う座標系について見ていきましょう。
直交座標系（Cartesian coordinate system）
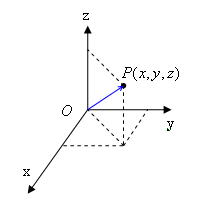一本の直線上の点の位置をを指定するのにはひとつの値を示せば良いでしょう。ものさしで位置を読む時の要領です。地図上の位置を示す時などの様に平面上の点の位置を示すには、直角に交わる2本の数直線を用い、
デカルト（René Descartes）によって発明され最も良く見る座標系です。x 軸と y 軸が直角に交わり、さらに z 軸がこれらに直角に交わるように取りますが、z 軸の取り方には２通りあって、（フレミングの左手の法則の形にした時）右手の親指、人差し指、中指の順に、x 軸、y 軸、z 軸となる場合を右手座標系（右手系）と呼びます。逆に，左手の親指、人差し指、中指の順に、x 軸、y 軸、z 軸となる場合を左手座標系（左手系）と呼びます。ここでは右手座標系を採用します。（左手座標系は Microsoft DirectX などで採用されています。）
この時、物の位置を表すのには、それぞれの軸の向きの基本ベクトル（単位ベクトル）を 
,
,
とすると
 |
（１） |
の様に表します。この３つの変数の組を使って位置を指定します。またこの原点 O から点 P に向かうベクトル r の事を位置ベクトルと言います。
極座標系（Polar coordinate system）
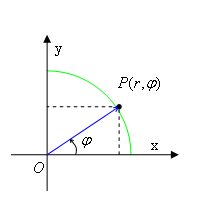後に紹介する球座標系と区別して「２次元極座標」
この座標系は円上の点を表すのに便利です。半径 a の円周上の点は全て
２次元の平面上の点の位置を原点 O からの距離 r と x 軸の正の方向から測った角度 φ で表します。また、基本ベクトルは原点 O から点 P に向かう単位ベクトルを 
とし、 に直交し角度 φ の正の方向に 
を取ります。これらを使うと
 |
（２） |
で表す事ができます。二体問題ではこの座標系を使います。また、デカルト座標系との対応は
 |
となります。（問）この様になる事を示せ。
円筒座標系（Cylindrical Polar Coordinates）
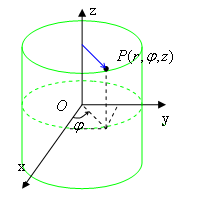先の極座標系に z 軸を付け加えたものです。
r = (r ,θ ,z )
この座標系は直線状の電荷分布の時の電場を表す時などに便利です。また、デカルト座標系との対応は
 |
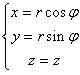となります。（問）この様になる事を示せ。
球座標系（Spherical Polar Coordinates）
原点 O からの距離 r 、x 軸の正の方向から測った角度 φ 、z 軸の正の方向から測った角度 θ を使って表します。
r = (r ,θ ,φ )
球対称性を持った系を表すのに便利です。また、デカルト座標系との対応は
 |
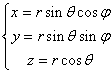となります。（問）下の図を参照してこの様になる事を示せ。
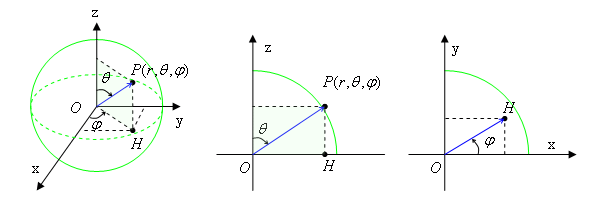
関連項目
ベクトル｜ベクトルの基本演算｜基本ベクトルの時間微分｜重積分｜ガウスの法則