ガウスの法則とは?
ガウスの法則とは電荷と電場の関係を表す法則です。ある適当な領域を考えて、その中にある電荷の総和とそこから出てくる電場の強さが比例するという事を言っています。
この事を式で表してやると
| (1) |
と表せることができる。(これは積分形)それぞれの記号の意味を下に列挙してみる。
| E | : | 電場を表す。これはベクトル量である。 |
|---|---|---|
| dS | : | 面素ベクトル。デカルト座標では dS = n dx dy などと表される。 |
| ε 0 | : | 真空の誘電率 |
| ρ | : | 電荷密度。問題によっては線電荷密度や面電荷密度ともなる。 |
| dv | : | 微小体積要素。デカルト座標では dv = dx dy dz |
これらの詳細は各ページを参照してもらいたい。(これから整備していきますm(__)m)
左辺の意味について考えてみよう。積分範囲を表す S は任意の閉曲面である。問題によって適切に選んでやる必要がある。例えば点電荷ではそれを中心に持つ球を考えてやる。E ・dS は電場ベクトルと微小面素ベクトルの内積である。つまり、電気力線がその面素を垂直に貫く本数を表している。これを全表面に対して積分してやると閉曲面 S から出てくる電気力線の数になる。
次に右辺を考える。左辺で任意の閉曲面 S を考えてやったが、それに囲まれた領域を V とする。電荷密度 ρ で分布しているとすると微小体積 dv 内には ρdv の電荷がある。これを V 内で積分してやると V 内にある電荷の総和が求められる。
しかしこの計算ができるのは系の対称性が良い場合に限られる。対称性が悪いと積分ができないからだ。ここで以下のような条件を満たす閉曲面 S を選ぶことができれば簡単に計算できるだろう。
- 閉曲面 S 上で電場 E が常に一定である。
- 閉曲面 S と電場 E が常に垂直である。
こんな曲面が選べるためには電場の分布が簡単に分からなければならない。以下のように電荷が分布していれば良いだろう。
- 無限に長い直線状(円筒状)に分布している。
- 点状(球状)に分布している。
- 無限に広い平面状(厚さがあっても良い)に分布している。
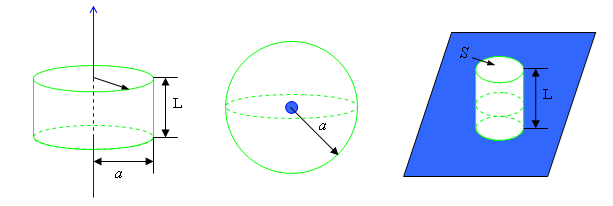
上の図で、電荷は青色の領域に分布していて、閉曲面を S は緑色の線で示される曲面の境界、領域を V はそれに囲まれた所である。
このようにガウスの法則が使えるのはかなり限られた状況でしかないのが分かるだろう。いつでも使える万能な物ではないのだ。そのような時にはクーロンの法則を使ってやらなくてはならないが、ガウスの法則が使える時には劇的に簡単に計算できる。
例題
(1)式はそのままでは何をして良いのかまったく解らないので、それぞれを具体的に書き直してやる事を考える。ここでやらなくてはいけないのは
- 対称性を考慮して、どのように座標を取ってやるのが良いかを考える。
- 適切な領域を考えてやる。
- それを基に面素ベクトル・微小体積要素を書いてやる。
- 問題の条件から電荷密度 ρ を求める。
ここまでやってやれば後は重積分の問題だ。では、実際に解いてみよう。
今回は半径 a の導体球殻に電荷 Q が一様に分布している。(どこかに偏っている理由は無いと思われる。)そしてこの球をどの方向から見ても性質は変わらない。このような時には球座標系(3次元極座標系)をとってやると簡単になる。(ここら辺の事情についてはいずれ別ページにまとめようと思う。)これが疑わしいと思う人はクーロンの法則を使って計算してやっても同じ結果が導ける。
関連項目
座標系|座標変換|重積分|ガウスの定理