問題
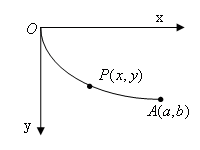17世紀のベルヌーイ（Jean Bernoulli (1667-1748) ベルヌーイの名のつく人は沢山居る）によって提起されニュートン等にあっさり解かれて落胆したと言う問題ですが、ノーヒントで解ける人は殆ど居ないでしょう。ちなみに上の英文字はブラッキストクローンと読みます。
重力場の中で質点を曲線に沿って落下させます。鉛直面 Oxy 内の原点 O から点 A に向かって落下する時、落下時間が極小になるように曲線の形を決定せよ。
変分法を使って解く
落下時間を求める
まず、点 P における速さは力学的エネルギー保存則 
より
 |
（１） |
です。また、点 P での曲線の長さは
 |
（２） |
と表されます。（１）式と（２）式より、点 O から点 A まで滑り落ちる時間 T は
 |
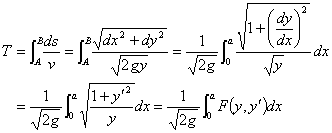（３） |
となります。
曲線の満たす方程式を求める
これから曲線の形を求めるには落下時間が最小となる関数 .png){kind=small}
を求めます。変分法の考え方より T が極値になるには、変分
 |
（４） |
が任意の 
について成り立てば良いのです。ここで 
とします。第１項目をテイラー展開して高次の微小量を無視すると
 |
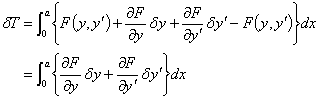（５） |
となります。ここで第２項目は部分積分をすれば
 |
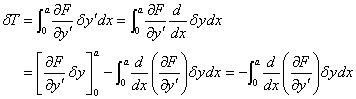（６） |
となるので
 |
（７） |
となり、これが任意の について成り立つので
 |
（８） |
の様な偏微分方程式の形で曲線の充たすべき条件を導けました。この方程式を解く為に（３）式を代入します。
 |
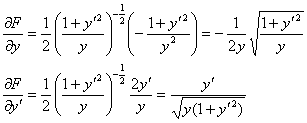（９） |
ここで 
を計算するのに対数微分法を使ってみます。両辺の自然対数を取ります。
 |
（10） |
両辺を 
で微分すると
 |
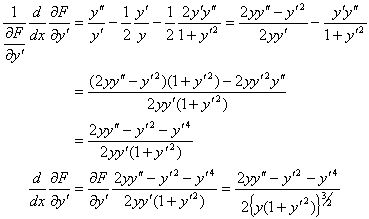（11） |
となるので、（８）式は
 |
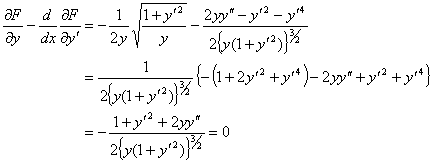（12） |
となります。結局、微分方程式
 |
（13） |
が得られました。
微分方程式を解く
と言っても（自分には）解けません。非線形の微分方程式ですからね。とりあえずエネルギー積分の時と同様に両辺に y ' をかけると
 |
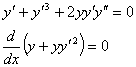（14） |
となるので積分すれば（問）（14）式で、下の式の微分を実行すると上の式になる事を確かめよ。
 |
（15） |
が得られます。この微分方程式はサイクロイド曲線を解に持つそうです。
 |
が（15）式の解になっている事は代入すれば確かめられます。（問）では確かめてみよう！こうして最速降下曲線はサイクロイド曲線である事が分かりました。
関連項目
サイクロイド曲線｜