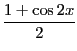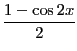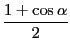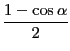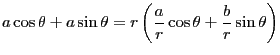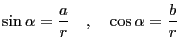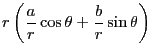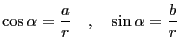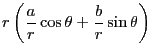三角関数の公式は教科書に沢山載っていて暗記するのはとても大変である。「咲いたコスモスコスモス咲いた」などと言った早覚えも有るが、忘れてしまえばそれまでで、とても賢い方法とは言えない。ここでは最小限の知識からスタートして多くの公式を導く事にしよう。
以下では幾つかの問題を設定し、多くの三角関数公式を導いていこう。現実的には三角関数の定義と加法定理を知っていれば十分である。これらから様々な公式を導く事が可能。
- a.
- まずは三角関数を定義し、加法定理を導こう。
- 1.
- 三角関数の定義を述べよ。また、
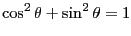 |
(12.1) |
を示せ。
- 2.
- 式(12.1)から
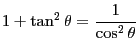 を導け。
を導け。
- 3.
- 絶対値が1で偏角が
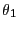 である複素数
である複素数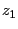 を
を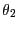 だけ回転した点を
だけ回転した点を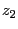 とする。すると
と表される。一方、
とする。すると
と表される。一方、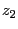 は
は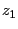 を
を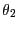 だけ回転した点なので
とも表せる。これを計算し、加法定理
だけ回転した点なので
とも表せる。これを計算し、加法定理
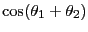 |
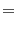 |
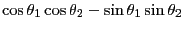 |
(12.2) |
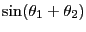 |
 |
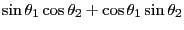 |
(12.3) |
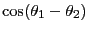 |
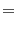 |
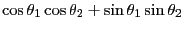 |
(12.4) |
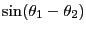 |
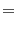 |
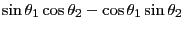 |
(12.5) |
を導け。
- b.
- 次に加法定理から様々な公式を導いていく。
- 1.
- 2倍角の公式を導出せよ。
- 2.
- 2倍角の公式より、半角の公式を導出せよ。
- 3.
- 和から積への変換公式を導出せよ。
- 4.
- 積から和への変換公式を導出せよ。
- 5.
- 三角関数の合成公式を導出せよ。
- 6.
- 3倍角の公式を導出せよ。
- 7.
- ド・モアブルの定理
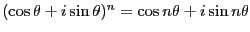 を使うと
を使うと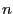 倍角の公式が導ける。これを用いて2倍角の公式と3倍角の公式を導け。ここで
倍角の公式が導ける。これを用いて2倍角の公式と3倍角の公式を導け。ここで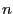 は整数である。1
は整数である。1
- a.
- 1.
- 先ず、始めに三角関数を定義する。
 AOBが
AOBが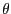 の直角三角形AOBを考える。この時の三角関数の定義は
の直角三角形AOBを考える。この時の三角関数の定義は
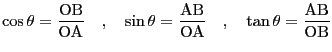 |
(12.6) |
となる。しかしこの定義では
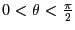 の範囲でしか使えない。そこで、点Oを中心とし、点Aを通る円を考える。そしてこの円周上を点Aが動くものとする。すると任意の
の範囲でしか使えない。そこで、点Oを中心とし、点Aを通る円を考える。そしてこの円周上を点Aが動くものとする。すると任意の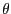 で三角関数が定義できる。
2
で三角関数が定義できる。
2
次に
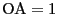 とすると三平方の定理より
とすると三平方の定理より
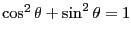 が示せる。この関係式は
が示せる。この関係式は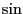 と
と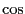 を相互に変換する時に良く使う。
を相互に変換する時に良く使う。
- 2.
- 式(12.1)の両辺を
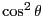 で割れば求める式
で割れば求める式
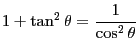 になる。
になる。
- 3.
- 計算すると
となる。それと
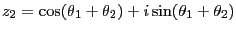 の実部と虚部を比較すると式(12.2)、式(12.3) が求まる。
の実部と虚部を比較すると式(12.2)、式(12.3) が求まる。
次に、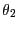 を
を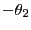 で置き換えると式(12.4)、式(12.5)が得られる。
3
で置き換えると式(12.4)、式(12.5)が得られる。
3
- b.
- 1.
- 式(12.2),式(12.3)で
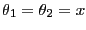 と置くと
と置くと
となり、これが2倍角の公式である。
- 2.
- 2倍角の公式(12.8)で式(12.1)を使うと
と変形できる。これを整理するとそれぞれ
が得られる。ここで の置き換えをすれば
の置き換えをすれば
となり、お馴染みの半角の公式が得られる。
- 3.
- これは加法定理の4つの式を適当に組み合わせる事で得られる。
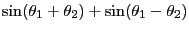 |
 |
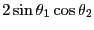 |
(12.16) |
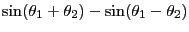 |
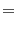 |
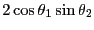 |
(12.17) |
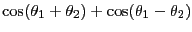 |
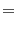 |
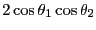 |
(12.18) |
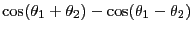 |
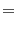 |
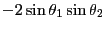 |
(12.19) |
この式が和から積・積から和への変換公式その物だと思っても差し支えない。ここで見慣れた形に書き換えてみよう。
と置くと上の式はそれぞれ
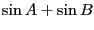 |
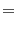 |
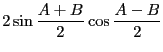 |
(12.20) |
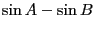 |
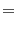 |
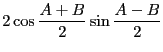 |
(12.21) |
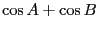 |
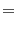 |
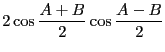 |
(12.22) |
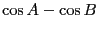 |
 |
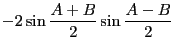 |
(12.23) |
と書き換えられる。これが和から積への変換公式である。
- 4.
- 上の式(12.16)〜式(12.19)をそのまま使えば良い。
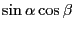 |
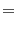 |
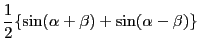 |
(12.24) |
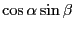 |
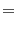 |
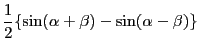 |
(12.25) |
 |
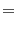 |
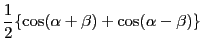 |
(12.26) |
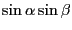 |
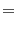 |
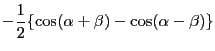 |
(12.27) |
ここで文字は適当に置き換えた。これが積から和への変換公式である。
- 5.
- 三角関数の合成公式を導出する。
と変形する。ここで
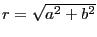 と置いた。ここで
と置くと上の式は
と置いた。ここで
と置くと上の式は
となり合成公式が導けた。ここで最後の変形は加法定理の式(12.3)を用いた。 この公式は良く用いられる。また、
と置くと上の式は
とも書ける。ここで最後の変形は加法定理の式(12.4)を用いた。
- 6.
- 加法定理と2倍角の公式より
となる。また、
が求まる。
- 7.
- 上の式で
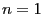 の時は自明だろう。
の時は自明だろう。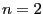 の時は
の時は
となり、この実部と虚部を比較すれば2倍角の公式がでる。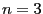 とすれば同様に
とすれば同様に
となり、この実部と虚部を比較すれば3倍角の公式がでる。
こうして多くの公式は加法定理から導出できる事を見た。これで教科書に大量に載っている公式を無駄に暗記する必要は無くなった。この分野には限らないが、『定義』は考えても出てこないので覚えるしかない。しかし『公式』は知っていると便利だが始めから暗記するべきものではない。具体的な問題を解く中で良く使うものについては覚えてゆけばよい。
- ...は整数である。1
- 平成17年現在、高校の学習指導要領では複素数平面は範囲外だそうだ。それでも上の式を認めれば計算は出来る。
- ...で三角関数が定義できる。
2
- この様な定義をすると三角関数と呼ぶよりは円関数と呼んだ方が良いかもしれない。
- ...eq4)が得られる。
3
- この公式を得るのには幾何学的な方法もある。そちらから求めるのが筋かもしれないが、少し考え難いのでここではこちらを採用した。


: この文書について...
: 数学の基礎
: 11 特集!三角形(工事中)
n_U-ki
平成17年9月14日
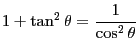 を導け。
を導け。
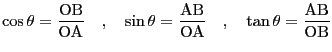
![]() とすると三平方の定理より
とすると三平方の定理より
![]() が示せる。この関係式は
が示せる。この関係式は![]() と
と![]() を相互に変換する時に良く使う。
を相互に変換する時に良く使う。
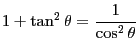 になる。
になる。
![]() を
を![]() で置き換えると式(12.4)、式(12.5)が得られる。
3
で置き換えると式(12.4)、式(12.5)が得られる。
3