- 階段型ポテンシャル
- 井戸型ポテンシャル
- 箱型ポテンシャル
- δ‐関数ポテンシャル
- 調和振動子
- 水素原子
以下の項目では束縛状態の時を考えるので解となる波動関数が 
の様に座標依存の項と時間依存の項に変数分離ができる事を前提とします。この時のエネルギー固有値方程式の固有値問題を解くことになります。
ここでこの様なポテンシャルを考えるのは現実の現象を近似的に表現して比較的簡単に解ける物を考えたかったからです。
波動関数が変数分離できる時
ポテンシャル .png){kind=small}
の存在する３次元空間での質量 m の粒子に対する Schrödinger 方程式
 |
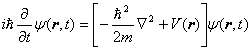（１） |
について、（１）式を満たす波動関数が のように時間依存の項と座標依存の項に変数分離できる時、（１）式は
 |
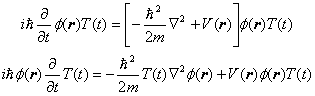（２） |
となります。両辺を 
で割ると
 |
（３） |
となり、左辺は t だけの関数で右辺は 
だけの関数になっています。（３）式が恒等的に成り立つためには、 t の関数でも無く の関数でも無い、つまり定数によって結ばれていなくてはなりません。この定数を E とすると次のようになります。
 |
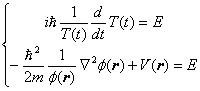（４） |
この定数 E の事をエネルギー固有値と呼びます。さらに（４）式を整理して
 |
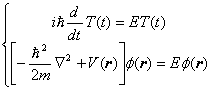（５） |
とする。この時の下の式の事を時間に依存しない Schrödinger 方程式または Hamiltonian 演算子に対するエネルギー固有値方程式と呼びます。
（５）式の上の式は変数分離型微分方程式なので
 |
（６） |
となってすぐに解く事が出来ます。後は下の式を解いて .png){kind=small}
を求めれば波動関数を求める事が出来ますが、上の式ほど簡単には解けません。以下のトピックではこのエネルギー固有値方程式の固有値問題を解く事と、それぞれの系に固有の問題を調べていく事にします。