| →次へ[井戸型ポテンシャル] | ←前へ[束縛状態のエネ…] | ↑量子力学 | ↑トップへ戻る |
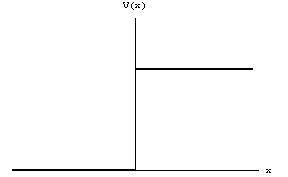
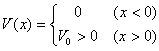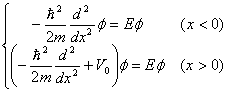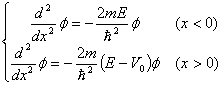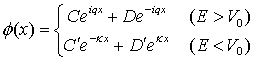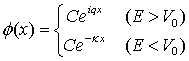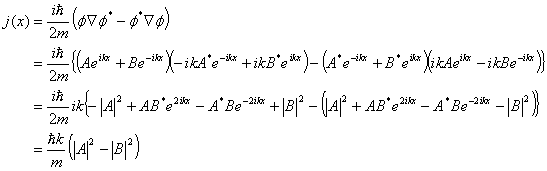階段型ポテンシャルとはその名の通り、階段の様に有限の飛びがあるポテンシャルの事です。（右図参照）この図では 
の時にはポテンシャルがゼロで何も無いのと同じだが、
ではある有限の値を持っています。ここに の方向からエネルギー E を持った質量 m の粒子が飛んで来た時の事を考えてみます。
このモデルは金属内の自由電子に対する近似として使われます。金属内では完全に自由に運動でき、表面では内部に押し戻すような力が働くと言う事を表現しています。
古典的にはこのポテンシャルの壁で跳ね返されるか飛び越えられるかであるが、量子力学ではこの様にはならない。エネルギーが高い時にはポテンシャルの向こうに進んで行けるがエネルギーが低い時にはどうだろう。確率密度を計算すると反射する物の他に の領域にも存在してる事になる。これはトンネル効果として実際に観測されている。トンネル効果ダイオード(江崎ダイオード)はこの効果を応用したものだ。
これから、以下の様にして階段型ポテンシャルがあった時の粒子の振る舞いを考えてみよう。
ポテンシャルが以下の様に与えられている。
 |
（１） |
ここに の方向からエネルギー E > 0 を持った質量 m の粒子が飛んで来た。この時のエネルギー固有値方程式は
 |
（２） |
と書ける。（２）式を整理すると
 |
（３） |
の様になる。これはどちらも２階の定数係数線形微分方程式である。上の式は 
とおけば波動方程式は
 |
（４） |
となる。（A、B は任意定数）一方、下の式は簡単の為に E と 
の大小で場合分けしておこう。ここで 
、
とおけば、（３）式の下の式の解は以下のように書ける。
 |
（５） |
ここで、波動関数の確率解釈が出来るためには波動関数は無限遠点で 0 に収束しなければならない。と言う事は の時に発散しない為には D ' = 0 でなくてはならない。また、 の領域では負の向きに進む波は考えない事にすると D = 0 となる。これらより結局
 |
（６） |
となる。以上で波動関数が未知数を含んだ形で求まった。
の時の確率流密度を計算すると
 |
（１） |
となる。 の時は
| →次へ[井戸型ポテンシャル] | ←前へ[束縛状態のエネ…] | ↑量子力学 | ↑トップへ戻る |