3次元空間中の質量 m の位置座標を r = (x ,y ,z ) とする。この時のシュレーディンガー方程式とその複素共役を取った物を用意します。
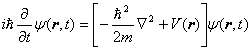 |
(1) |
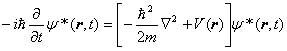 |
(2) |
そして、確率密度関数の時間微分を計算します。すると
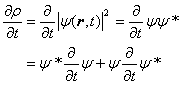 |
(3) |
となります。ここで(1)(2)式を使って波動関数の時間微分を書き換えて
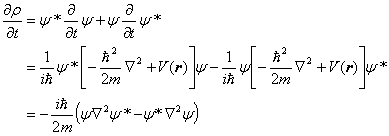 |
(4) |
と、計算できます。ここで
| (5) |
を使うと(問)左辺の微分を実行して右辺になる事を確かめよ。(4)式は
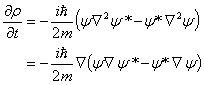 |
(6) |
となります。ここで確率密度の流れ(the flux dencity of probability)(あるいは確率の流れの密度)を
| (7) |
で定義すると結局(3)式は
| (8) |
で表される事が分かりました。この式の事を連続の方程式と言って質量や電荷に対しても同様に成り立ちます。