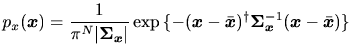- 期待値(exception)
![$\displaystyle E_x [g(x)] = \int_{-\infty}^{\infty} g(\xi) p_x(\xi) d\xi$](img104.png) |
(61) |
- 平均(average, mean value)
![$\displaystyle \bar{x} = E_x [x] = \int_{-\infty}^{\infty} \xi p_x(\xi) d\xi$](img105.png) |
(62) |
- 分散(variance)
![$\displaystyle \sigma_x^2 = E_x [(x-\bar{x})^2] = \int_{-\infty}^{\infty} (\xi-\bar{x})^2 p_x(\xi) d\xi$](img106.png) |
(63) |
- 標準偏差(standard deviation)
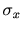
- モーメント(moment)
![$\displaystyle E_x [x^m] = (-i)^m \left. \frac{d^m \phi_x(\zeta)}{d\zeta^m}\right \vert _{z=0} = (-i)^m \phi_x^{(m)}(0)$](img108.png) |
(64) |
条件付き確率 (Conditional probability) とは、ある事象Bが起こるという条件の下で別の事象Aの確率をいい、これを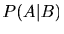 または
または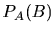 と書く。
と書く。
エルゴード過程(elgodic process)の基本的な考え方は集合平均(ensamble average)を時間平均(time average)で置き換える事である。
定常過程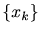 から任意の関数を用いて得られる新たな過程
から任意の関数を用いて得られる新たな過程
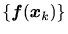 の平均過程がその一つの標本過程
の平均過程がその一つの標本過程
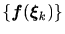 によって
によって
![$\displaystyle E_{\bm{x}_k} [\bm{f}(\bm{x}_k)] = \lim_{L\rightarrow \infty} \frac{1}{2L+1} \sum_{i=-L}^{L} \bm{f}(\bm{\xi}_{k+i})$](img113.png) |
(65) |
と表わせる時、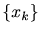 はエルゴード性(elgodicity)
を持つという。また、時間平均と集合平均が等しい過程をエルゴード過程という。
はエルゴード性(elgodicity)
を持つという。また、時間平均と集合平均が等しい過程をエルゴード過程という。
確率過程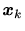 において、任意の
において、任意の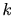 と
と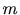 に対して
に対して
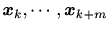 の結合確率密度関数が存在し、かつGauss分布
の結合確率密度関数が存在し、かつGauss分布
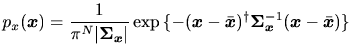 |
(66) |
であれば、
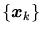 をGauss過程と呼ぶ。
をGauss過程と呼ぶ。
時刻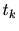 における
における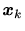 が一つ前の時刻の状態
が一つ前の時刻の状態
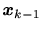 だけに依存し、それ以上前の状態
だけに依存し、それ以上前の状態
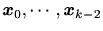 には無関係
には無関係
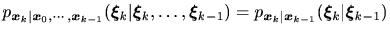 |
(67) |
であるとき、確率過程
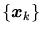 を1次のMarkov過程と呼ぶ。結合確率密度関数はBayesの定理より
を1次のMarkov過程と呼ぶ。結合確率密度関数はBayesの定理より
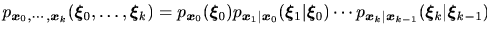 |
(68) |
と表される。また、2次のMarkov過程は
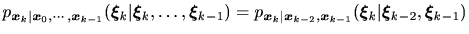 |
(69) |
で定義され、高次のMarkov過程も同様に定義できる。
Copyright © 2004-2011 RandomWalker All Rights Reserved.
yfa68798 atto nifty.com
![$\displaystyle E_x [g(x)] = \int_{-\infty}^{\infty} g(\xi) p_x(\xi) d\xi$](img104.png)
![$\displaystyle \bar{x} = E_x [x] = \int_{-\infty}^{\infty} \xi p_x(\xi) d\xi$](img105.png)
![$\displaystyle \sigma_x^2 = E_x [(x-\bar{x})^2] = \int_{-\infty}^{\infty} (\xi-\bar{x})^2 p_x(\xi) d\xi$](img106.png)
![$\displaystyle E_x [x^m] = (-i)^m \left. \frac{d^m \phi_x(\zeta)}{d\zeta^m}\right \vert _{z=0} = (-i)^m \phi_x^{(m)}(0)$](img108.png)
![$\displaystyle E_{\bm{x}_k} [\bm{f}(\bm{x}_k)] = \lim_{L\rightarrow \infty} \frac{1}{2L+1} \sum_{i=-L}^{L} \bm{f}(\bm{\xi}_{k+i})$](img113.png)