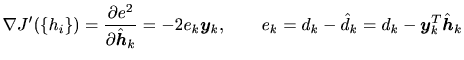線形フィルタの出力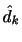 は入力信号
は入力信号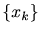 とインパルス応答
とインパルス応答
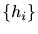 の畳み込み(convolution)を用いて次のように書ける。
の畳み込み(convolution)を用いて次のように書ける。
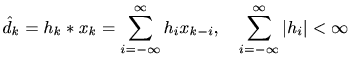 |
(1) |
つまり、線形フィルタの特性はインパルス応答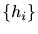 が決めている。
ここで、インパルス応答
が決めている。
ここで、インパルス応答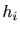 をz変換した物は伝達関数(transfar function)を表す。
をz変換した物は伝達関数(transfar function)を表す。
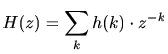 |
(2) |
Wienerフィルタは所望の信号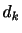 との平均2乗誤差
との平均2乗誤差
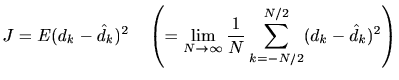 |
(3) |
を最小にする最適推定値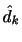 を出力するフィルタである。
Wienerフィルタにおいて入力信号と所望の信号にそれぞれ何を想定するかで表 1のように様々な働きを持ったフィルタが構成できる。
を出力するフィルタである。
Wienerフィルタにおいて入力信号と所望の信号にそれぞれ何を想定するかで表 1のように様々な働きを持ったフィルタが構成できる。
図 2:
平均二乗誤差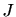 の最小値。
の最小値。
![\begin{figure}\begin{center}
%
\unitlength 0.1in
\begin{picture}( 32.6000, 27.7...
...8.0000){\makebox(0,0)[lb]{誤差曲面}}%
\end{picture}%
\end{center}
\end{figure}](img16.png) |
表 1:
Wienerフィルタの一般的な実現状況。ここで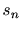 は観測系列に含まれる信号系列、
は観測系列に含まれる信号系列、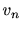 は雑音系列を表す。
は雑音系列を表す。
| 問題 |
入力信号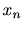 |
所望信号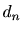 |
| 雑音中の信号のフィルタリング |
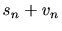 |
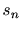 |
| 雑音中の信号の予測 |
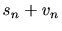 |
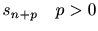 |
| 雑音中の信号の平滑化 |
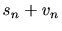 |
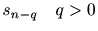 |
| 線形予測 |
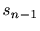 |
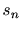 |
| 一般非線形問題 |
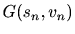 |
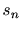 |
例えば、入力信号は源信号とノイズの和
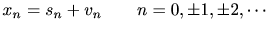 |
(4) |
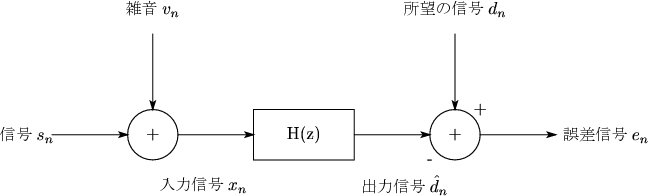
で表すと図 3のようなブロック図が書ける。
図 3:
Wienerフィルタの構成例。ここでは雑音中の信号のフィルタリングする場合を示す。
 |
以上より、Wienerフィルタの設計問題は式(3)を最小にするインパルス応答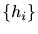 を探すことであり、最小値の求め方によりいくつかのアルゴリズムが提案されている。
を探すことであり、最小値の求め方によりいくつかのアルゴリズムが提案されている。
最終的に次の相関関数に関するWiener-Hopf方程式として表される。、
![$\displaystyle R_{dy} [ m ] = \sum_{i=-\infty }^{\infty } h_i^{\rm op} r_{yy} [ m-i ] = h_i^{\rm op} * r_{yy} [ m ] ,\qquad m \in \mathbb{Z}$](img26.png) |
(5) |
この方程式を満たす解(Wiener解)をインパルス応答
-
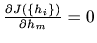 となる
となる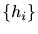 を求める
を求める
- 最急降下法により反復的に求める
- LMSアルゴリズム
ウィーナーフィルタは過去から未来に至るまでのすべての入力データ
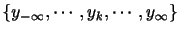 を必要としている。ところが、未来のデータを知ることは出来ないため、過去から現在までのデータ
を必要としている。ところが、未来のデータを知ることは出来ないため、過去から現在までのデータ
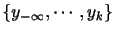 を用いて所望信号
を用いて所望信号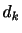 の最適推定値
の最適推定値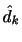 を求めなければならない。
を求めなければならない。
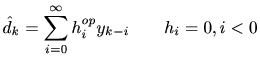 |
(6) |
最終的に次の相関関数に関するWiener-Hopf方程式として表される。、
![$\displaystyle R_{dy} [ m ] = \sum_{i=0 }^{\infty } h_i^{\rm op} r_{yy} [ m-i ] = h_i^{\rm op} * r_{yy} [ m ] ,\qquad m \in \mathbb{Z}$](img31.png) |
(7) |
因果的ウィーナーフィルタ(近似解)では、信号の統計量(相関関数)を事前に求める必要があるため、実時間処理には適さない。また、信号の統計量が設計段階と異なると、そのフィルタ係数は最適ではなくなる。
そこで、フィルタ係数をある初期値から適応的に少しずつ自己調整し、最終的に最適フィルタを実現するフィルタが考案された。このようなフィルタ係数の自己調整機能(適応アルゴリズム)を持ったデジタルフィルタを適応フィルタ(adaptive filter)と呼ぶ。
ここでは時間のかかる逆行列の計算などの代わりに、適当な初期値から出発し、最急降下法を用いて反復的に最小値を求める。
平均2乗誤差
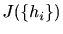 は最小値
は最小値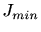 を用いて次のように表現できる。
を用いて次のように表現できる。
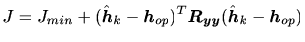 |
(8) |
これより平均2乗誤差
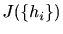 は単峰性だと分かる。よって最急降下方向
は単峰性だと分かる。よって最急降下方向
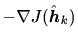 に反復的に係数
に反復的に係数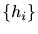 を更新していけばいずれWiener解
を更新していけばいずれWiener解
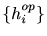 に収束すると考えられる。
に収束すると考えられる。
そこで、フィルタ係数
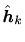 をある初期値
をある初期値
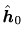 から次の漸化式に従って更新する。
から次の漸化式に従って更新する。
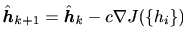 |
(9) |
この計算には逆行列の計算が含まれない。
ここで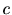 はステップサイズを表し、更新による修正量を決定する。
はステップサイズを表し、更新による修正量を決定する。
最急降下法を用いて逆行列の計算を省くことに成功した。LMSアルゴリズム(Least Mean Square algorithm)ではさらに期待値演算を除いた勾配を用いる。これは最急降下法における勾配を瞬時値で置換した方法と解釈できる。
LMSアルゴリズムでは最急降下法で用いた勾配
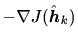 に代わって期待値演算を除いた次の勾配を用いる。
に代わって期待値演算を除いた次の勾配を用いる。
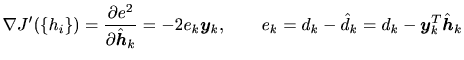 |
(10) |
大胆な扱いだが、その平均値(期待値)は最急降下法の勾配と一致し、フィルタ係数の期待値は最終的にWiener解と一致する。
Copyright © 2004-2011 RandomWalker All Rights Reserved.
yfa68798 atto nifty.com
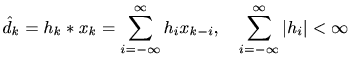
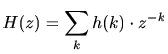
![]() を探すことであり、最小値の求め方によりいくつかのアルゴリズムが提案されている。
を探すことであり、最小値の求め方によりいくつかのアルゴリズムが提案されている。
![$\displaystyle R_{dy} [ m ] = \sum_{i=-\infty }^{\infty } h_i^{\rm op} r_{yy} [ m-i ] = h_i^{\rm op} * r_{yy} [ m ] ,\qquad m \in \mathbb{Z}$](img26.png)
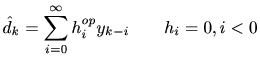
![$\displaystyle R_{dy} [ m ] = \sum_{i=0 }^{\infty } h_i^{\rm op} r_{yy} [ m-i ] = h_i^{\rm op} * r_{yy} [ m ] ,\qquad m \in \mathbb{Z}$](img31.png)
![]() は最小値
は最小値![]() を用いて次のように表現できる。
を用いて次のように表現できる。
![]() をある初期値
をある初期値
![]() から次の漸化式に従って更新する。
から次の漸化式に従って更新する。
![]() に代わって期待値演算を除いた次の勾配を用いる。
に代わって期待値演算を除いた次の勾配を用いる。