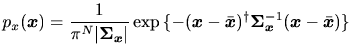Wienerフィルタ
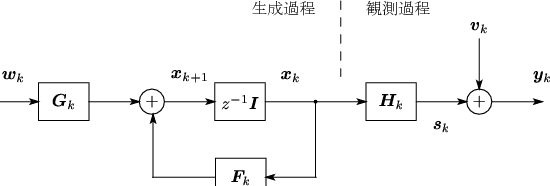
状態方程式と観測方程式。
図 5:
状態空間モデルのブロック線図。
 |
観測値
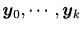 が与えられた時の
が与えられた時の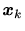 の最小分散推定値
の最小分散推定値
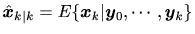 または
または
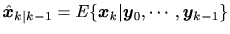 を求める問題をカルマンフィルタリング問題
カルマンフィルタリング問題(Kalman filtering problem)と言い、
その解を与えるアルゴリズムをカルマンフィルタ(Kalman filter)と呼ぶ。
を求める問題をカルマンフィルタリング問題
カルマンフィルタリング問題(Kalman filtering problem)と言い、
その解を与えるアルゴリズムをカルマンフィルタ(Kalman filter)と呼ぶ。
フィルタ方程式
カルマンゲイン
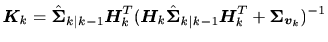 |
(15) |
誤差の共分散行列方程式
初期値
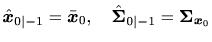 |
(18) |
図 7:
Kalmanフィルタのブロック線図。
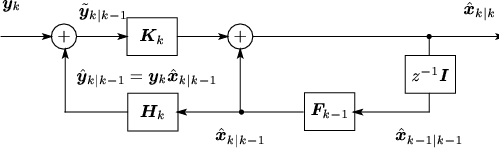 |
カルマンフィルタの1段予測値
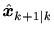 に関して整理しなおすと次のようにまとめられる。
に関して整理しなおすと次のようにまとめられる。
フィルタ方程式
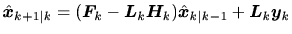 |
(19) |
カルマンゲイン
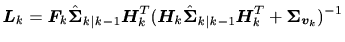 |
(20) |
誤差の共分散行列方程式
初期値
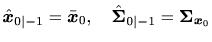 |
(22) |
1段予測型KalmanフィルタとKalmanフィルタは等価であり、
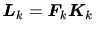 の関係がある。
の関係がある。
図 8:
1段予測型Kalmanフィルタのブロック線図。
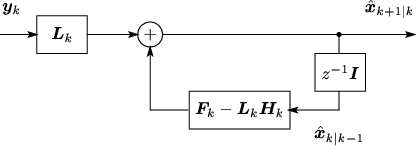 |
源信号
 と観測信号
と観測信号
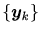 が結合Gauss性であるとき、Kalmanフィルタは非線形フィルタも含めて、あらゆるフィルタの中で最も最適なフィルタであった。しかし、現実の問題ではGauss性の仮定は必ずしも保証されない。そこで、非Gauss性の場合への拡張を行う。
が結合Gauss性であるとき、Kalmanフィルタは非線形フィルタも含めて、あらゆるフィルタの中で最も最適なフィルタであった。しかし、現実の問題ではGauss性の仮定は必ずしも保証されない。そこで、非Gauss性の場合への拡張を行う。
フィルタ方程式
カルマンゲイン
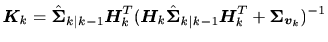 |
(25) |
誤差の共分散行列方程式
初期値
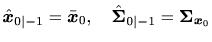 |
(28) |
Kalmanフィルタを導入した際にはGauss性を仮定してフィルタを構築したが、Gauss性の無い場合にもそのまま成り立つ事が分かった。
ただし、Gauss性でない場合のKalmanフィルタは、あらゆるフィルタの中で最も最適なフィルタであるとは限らない。
データ通信や計測分野などへの応用では、システムの状態空間モデルは複素数で定義した方が都合がよい。そこで、Kanlamフィルタを複素数へ拡張する。
ここで、入力信号にはGauss性に代わって複素Gauss性
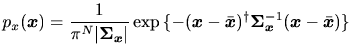 |
(29) |
を仮定する。
フィルタ方程式
カルマンゲイン
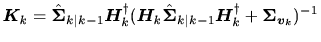 |
(32) |
誤差の共分散行列方程式
初期値
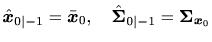 |
(35) |
通常のカルマンフィルタとの違いは各ベクトルと行列の成分が複素数になっている事だけである。そのため転置行列はエルミート行列
で置き換えた。
図 9:
外部入力を持つ状態空間のブロック線図。
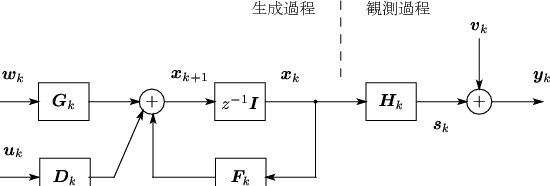 |
フィルタ方程式
カルマンゲイン
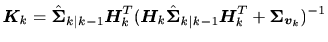 |
(38) |
誤差の共分散行列方程式
初期値
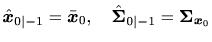 |
(41) |
図 10:
外部入力を持つKalmanフィルタのブロック線図。
![\begin{figure}\begin{center}
%
\unitlength 0.1in
\begin{picture}( 42.7000, 16.4...
...ebox(0,0)[lt]{$\hat{\bm{u}}_{k-1}$}}%
\end{picture}%
\end{center}
\end{figure}](img81.png) |
フィルタ方程式
カルマンゲイン
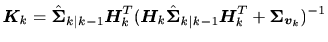 |
(44) |
誤差の共分散行列方程式
初期値
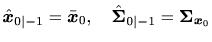 |
(47) |
非線形確率システムに対する準最適フィルタ。
フィルタ方程式
カルマンゲイン
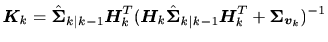 |
(50) |
誤差の共分散行列方程式
初期値
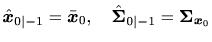 |
(53) |
Copyright © 2004-2011 RandomWalker All Rights Reserved.
yfa68798 atto nifty.com
![]() の関係がある。
の関係がある。